Calculus Derivative Cheat Sheet
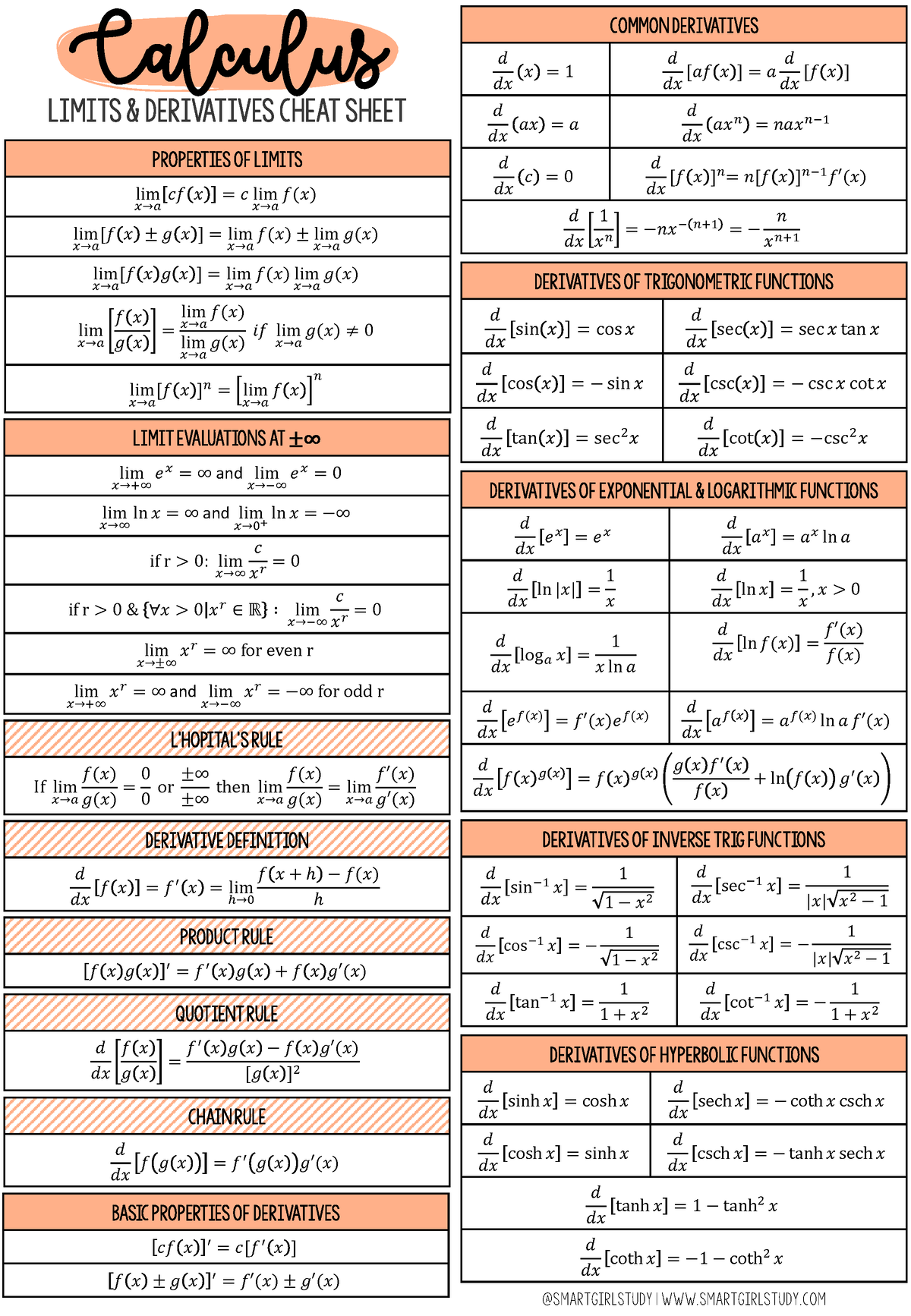
Calculus Derivative Cheat Sheet - The chain rule applied to some specific functions. Write down equation relating quantities and differentiate with respect to t using implicit differentiation (i.e. \frac {d} {dx}\left (e^ {x})=e^ {x} \frac {d} {dx}\left (\log (x))=\frac {1} {x\ln (10)} \frac {d} {dx}\left (\log_ {a} (x))=\frac {1} {x\ln (a)} \frac {d}. ¢ f ¢¢ ( x ) = ( f ¢ ( x ) ). Add on a derivative every.
The chain rule applied to some specific functions. Add on a derivative every. Write down equation relating quantities and differentiate with respect to t using implicit differentiation (i.e. ¢ f ¢¢ ( x ) = ( f ¢ ( x ) ). \frac {d} {dx}\left (e^ {x})=e^ {x} \frac {d} {dx}\left (\log (x))=\frac {1} {x\ln (10)} \frac {d} {dx}\left (\log_ {a} (x))=\frac {1} {x\ln (a)} \frac {d}.
¢ f ¢¢ ( x ) = ( f ¢ ( x ) ). The chain rule applied to some specific functions. \frac {d} {dx}\left (e^ {x})=e^ {x} \frac {d} {dx}\left (\log (x))=\frac {1} {x\ln (10)} \frac {d} {dx}\left (\log_ {a} (x))=\frac {1} {x\ln (a)} \frac {d}. Add on a derivative every. Write down equation relating quantities and differentiate with respect to t using implicit differentiation (i.e.
Calculus derivatives rules and limits cheat sheet eeweb Artofit
\frac {d} {dx}\left (e^ {x})=e^ {x} \frac {d} {dx}\left (\log (x))=\frac {1} {x\ln (10)} \frac {d} {dx}\left (\log_ {a} (x))=\frac {1} {x\ln (a)} \frac {d}. Write down equation relating quantities and differentiate with respect to t using implicit differentiation (i.e. The chain rule applied to some specific functions. Add on a derivative every. ¢ f ¢¢ ( x ) =.
Calculus DERIVATIVES Study Outline 1 Page Cheat Sheet Digital File Only
Add on a derivative every. \frac {d} {dx}\left (e^ {x})=e^ {x} \frac {d} {dx}\left (\log (x))=\frac {1} {x\ln (10)} \frac {d} {dx}\left (\log_ {a} (x))=\frac {1} {x\ln (a)} \frac {d}. ¢ f ¢¢ ( x ) = ( f ¢ ( x ) ). Write down equation relating quantities and differentiate with respect to t using implicit differentiation (i.e. The.
Derivative cheat sheet Cheat Sheet Mathematical Analysis Docsity
The chain rule applied to some specific functions. Write down equation relating quantities and differentiate with respect to t using implicit differentiation (i.e. ¢ f ¢¢ ( x ) = ( f ¢ ( x ) ). \frac {d} {dx}\left (e^ {x})=e^ {x} \frac {d} {dx}\left (\log (x))=\frac {1} {x\ln (10)} \frac {d} {dx}\left (\log_ {a} (x))=\frac {1} {x\ln (a)}.
Calculus Cheat Sheet Derivatives
Add on a derivative every. \frac {d} {dx}\left (e^ {x})=e^ {x} \frac {d} {dx}\left (\log (x))=\frac {1} {x\ln (10)} \frac {d} {dx}\left (\log_ {a} (x))=\frac {1} {x\ln (a)} \frac {d}. ¢ f ¢¢ ( x ) = ( f ¢ ( x ) ). The chain rule applied to some specific functions. Write down equation relating quantities and differentiate with.
Calculus DERIVATIVES Study Outline 1 Page Cheat Sheet Digital File Only
\frac {d} {dx}\left (e^ {x})=e^ {x} \frac {d} {dx}\left (\log (x))=\frac {1} {x\ln (10)} \frac {d} {dx}\left (\log_ {a} (x))=\frac {1} {x\ln (a)} \frac {d}. Add on a derivative every. ¢ f ¢¢ ( x ) = ( f ¢ ( x ) ). The chain rule applied to some specific functions. Write down equation relating quantities and differentiate with.
Calculus_Cheat_Sheet_All_Reduced.pdf Maxima And Minima Derivative
Add on a derivative every. ¢ f ¢¢ ( x ) = ( f ¢ ( x ) ). \frac {d} {dx}\left (e^ {x})=e^ {x} \frac {d} {dx}\left (\log (x))=\frac {1} {x\ln (10)} \frac {d} {dx}\left (\log_ {a} (x))=\frac {1} {x\ln (a)} \frac {d}. Write down equation relating quantities and differentiate with respect to t using implicit differentiation (i.e. The.
Application Of Derivatives Calculus
\frac {d} {dx}\left (e^ {x})=e^ {x} \frac {d} {dx}\left (\log (x))=\frac {1} {x\ln (10)} \frac {d} {dx}\left (\log_ {a} (x))=\frac {1} {x\ln (a)} \frac {d}. Add on a derivative every. Write down equation relating quantities and differentiate with respect to t using implicit differentiation (i.e. The chain rule applied to some specific functions. ¢ f ¢¢ ( x ) =.
Calculus Cheat Sheet i dont know la Limits & Derivatives Cheat
Add on a derivative every. ¢ f ¢¢ ( x ) = ( f ¢ ( x ) ). \frac {d} {dx}\left (e^ {x})=e^ {x} \frac {d} {dx}\left (\log (x))=\frac {1} {x\ln (10)} \frac {d} {dx}\left (\log_ {a} (x))=\frac {1} {x\ln (a)} \frac {d}. Write down equation relating quantities and differentiate with respect to t using implicit differentiation (i.e. The.
Matrix Derivative Cheat Sheet
Add on a derivative every. \frac {d} {dx}\left (e^ {x})=e^ {x} \frac {d} {dx}\left (\log (x))=\frac {1} {x\ln (10)} \frac {d} {dx}\left (\log_ {a} (x))=\frac {1} {x\ln (a)} \frac {d}. ¢ f ¢¢ ( x ) = ( f ¢ ( x ) ). The chain rule applied to some specific functions. Write down equation relating quantities and differentiate with.
Cheat Sheet Calculus Maxima And Minima Derivative
The chain rule applied to some specific functions. Write down equation relating quantities and differentiate with respect to t using implicit differentiation (i.e. \frac {d} {dx}\left (e^ {x})=e^ {x} \frac {d} {dx}\left (\log (x))=\frac {1} {x\ln (10)} \frac {d} {dx}\left (\log_ {a} (x))=\frac {1} {x\ln (a)} \frac {d}. Add on a derivative every. ¢ f ¢¢ ( x ) =.
Write Down Equation Relating Quantities And Differentiate With Respect To T Using Implicit Differentiation (I.e.
¢ f ¢¢ ( x ) = ( f ¢ ( x ) ). \frac {d} {dx}\left (e^ {x})=e^ {x} \frac {d} {dx}\left (\log (x))=\frac {1} {x\ln (10)} \frac {d} {dx}\left (\log_ {a} (x))=\frac {1} {x\ln (a)} \frac {d}. Add on a derivative every. The chain rule applied to some specific functions.