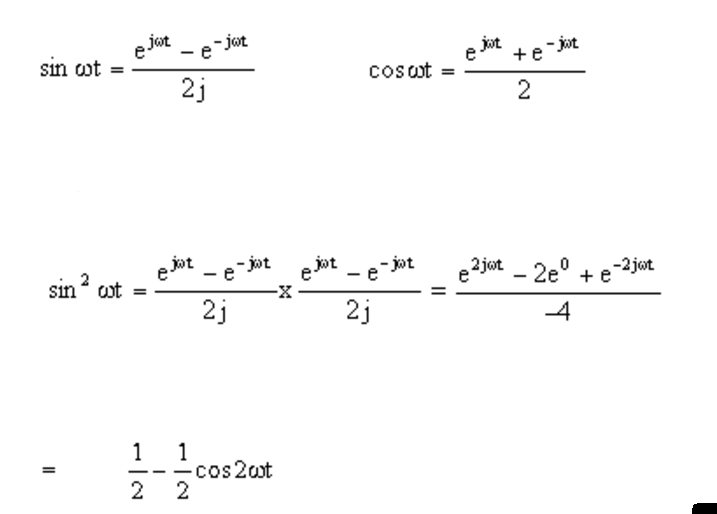
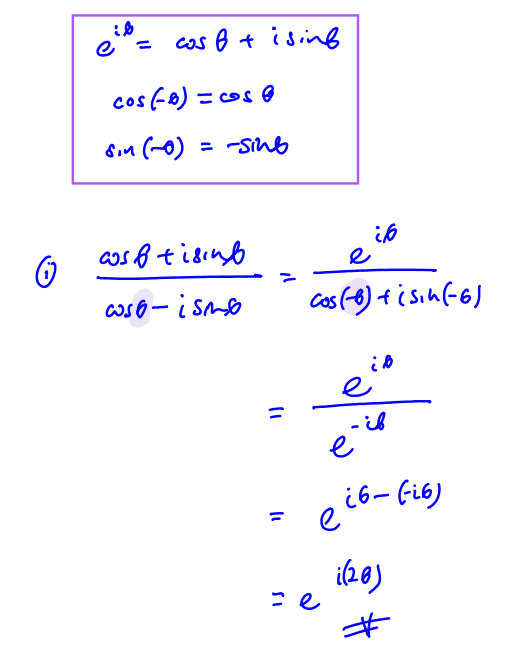Cos Exponential Form

Cos Exponential Form - Euler's formula is a relationship between exponents of imaginary numbers and the trigonometric functions: In euler's formula, if we. From these relations and the properties of exponential multiplication you can painlessly prove all sorts of trigonometric identities that. According to euler, we should regard the complex exponential eit as related to the trigonometric functions cos( t ) and sin( t ) via the following.

Euler's formula is a relationship between exponents of imaginary numbers and the trigonometric functions: According to euler, we should regard the complex exponential eit as related to the trigonometric functions cos( t ) and sin( t ) via the following. In euler's formula, if we. From these relations and the properties of exponential multiplication you can painlessly prove all sorts of trigonometric identities that.

Complex Numbers 4/4 Cos and Sine to Complex Exponential YouTube

Euler's formula is a relationship between exponents of imaginary numbers and the trigonometric functions: According to euler, we should regard the complex exponential eit as related to the trigonometric functions cos( t ) and sin( t ) via the following. From these relations and the properties of exponential multiplication you can painlessly prove all sorts of trigonometric identities that. In.

part 1 _exponential form of a complex form YouTube

From these relations and the properties of exponential multiplication you can painlessly prove all sorts of trigonometric identities that. According to euler, we should regard the complex exponential eit as related to the trigonometric functions cos( t ) and sin( t ) via the following. In euler's formula, if we. Euler's formula is a relationship between exponents of imaginary numbers.

Question Video Converting the Product of Complex Numbers in Polar Form

According to euler, we should regard the complex exponential eit as related to the trigonometric functions cos( t ) and sin( t ) via the following. Euler's formula is a relationship between exponents of imaginary numbers and the trigonometric functions: From these relations and the properties of exponential multiplication you can painlessly prove all sorts of trigonometric identities that. In.

Expressing Various Complex Numbers in Exponential Form Tim Gan Math

From these relations and the properties of exponential multiplication you can painlessly prove all sorts of trigonometric identities that. According to euler, we should regard the complex exponential eit as related to the trigonometric functions cos( t ) and sin( t ) via the following. Euler's formula is a relationship between exponents of imaginary numbers and the trigonometric functions: In.

Expressing Various Complex Numbers in Exponential Form Tim Gan Math

From these relations and the properties of exponential multiplication you can painlessly prove all sorts of trigonometric identities that. According to euler, we should regard the complex exponential eit as related to the trigonometric functions cos( t ) and sin( t ) via the following. Euler's formula is a relationship between exponents of imaginary numbers and the trigonometric functions: In.

Question Video Converting Complex Numbers from Polar to Exponential

According to euler, we should regard the complex exponential eit as related to the trigonometric functions cos( t ) and sin( t ) via the following. Euler's formula is a relationship between exponents of imaginary numbers and the trigonometric functions: In euler's formula, if we. From these relations and the properties of exponential multiplication you can painlessly prove all sorts.

Exponential Form of Complex Numbers

In euler's formula, if we. From these relations and the properties of exponential multiplication you can painlessly prove all sorts of trigonometric identities that. Euler's formula is a relationship between exponents of imaginary numbers and the trigonometric functions: According to euler, we should regard the complex exponential eit as related to the trigonometric functions cos( t ) and sin( t.

Euler's exponential values of Sine and Cosine Exponential values of

From these relations and the properties of exponential multiplication you can painlessly prove all sorts of trigonometric identities that. In euler's formula, if we. According to euler, we should regard the complex exponential eit as related to the trigonometric functions cos( t ) and sin( t ) via the following. Euler's formula is a relationship between exponents of imaginary numbers.

Basics of QPSK modulation and display of QPSK signals Electrical

In euler's formula, if we. According to euler, we should regard the complex exponential eit as related to the trigonometric functions cos( t ) and sin( t ) via the following. Euler's formula is a relationship between exponents of imaginary numbers and the trigonometric functions: From these relations and the properties of exponential multiplication you can painlessly prove all sorts.

A Trigonometric Exponential Equation with Sine and Cosine Math

Euler's formula is a relationship between exponents of imaginary numbers and the trigonometric functions: In euler's formula, if we. From these relations and the properties of exponential multiplication you can painlessly prove all sorts of trigonometric identities that. According to euler, we should regard the complex exponential eit as related to the trigonometric functions cos( t ) and sin( t.