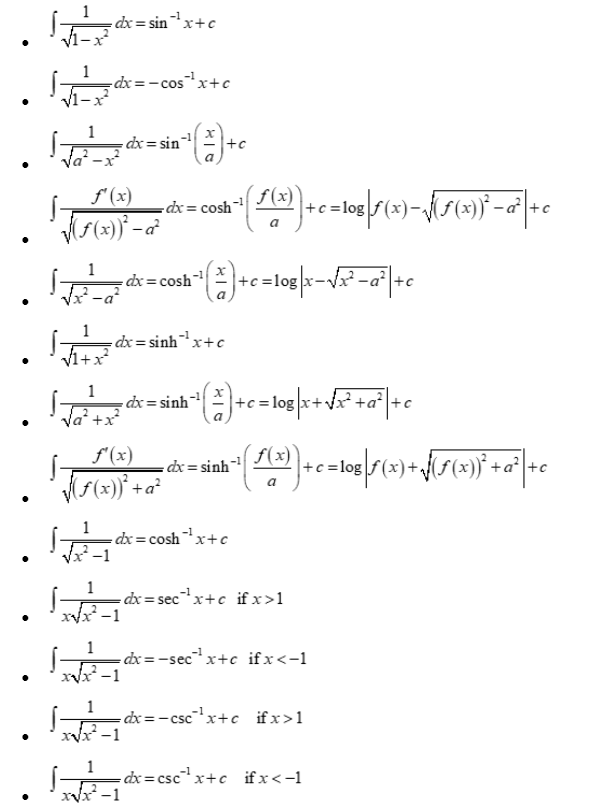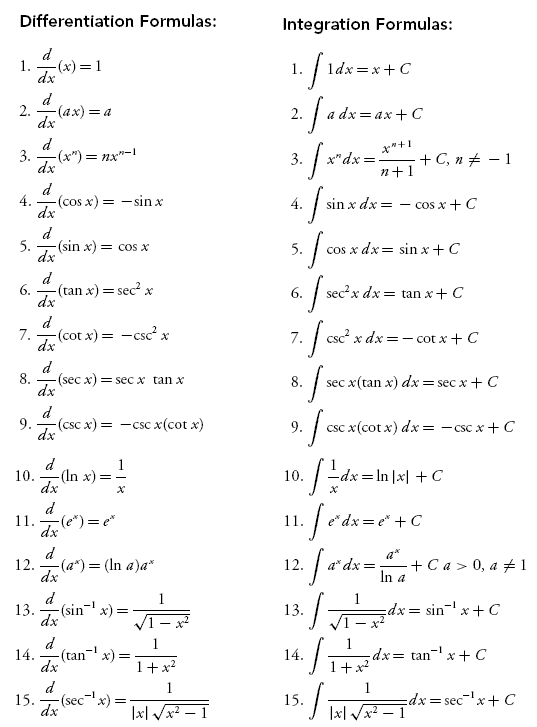Integral Rules Sheet

Integral Rules Sheet - Integrals with trigonometric functions z sinaxdx= 1 a cosax (63) z sin2 axdx= x 2 sin2ax 4a (64) z sinn axdx= 1 a cosax 2f 1 1 2; Integral is called convergent if the limit exists and has a finite value and divergent if the limit doesn’t exist or has infinite value. ⋅ (𝑥 ) 𝑥= ⋅∫ 𝑥 𝑥 ∫sum/difference. Integral of a constant \int f\left(a\right)dx=x\cdot f\left(a\right) take the constant out \int a\cdot f\left(x\right)dx=a\cdot \int f\left(x\right)dx. ( ) 𝑥=𝑥⋅ ( ) ∫taking a constant out: ′= −∫ ′ ∫integral of a constant: Cheat sheet for integrals 1.

( ) 𝑥=𝑥⋅ ( ) ∫taking a constant out: Integral of a constant \int f\left(a\right)dx=x\cdot f\left(a\right) take the constant out \int a\cdot f\left(x\right)dx=a\cdot \int f\left(x\right)dx. ⋅ (𝑥 ) 𝑥= ⋅∫ 𝑥 𝑥 ∫sum/difference. ′= −∫ ′ ∫integral of a constant: Integrals with trigonometric functions z sinaxdx= 1 a cosax (63) z sin2 axdx= x 2 sin2ax 4a (64) z sinn axdx= 1 a cosax 2f 1 1 2; Cheat sheet for integrals 1. Integral is called convergent if the limit exists and has a finite value and divergent if the limit doesn’t exist or has infinite value.

( ) 𝑥=𝑥⋅ ( ) ∫taking a constant out: Cheat sheet for integrals 1. ⋅ (𝑥 ) 𝑥= ⋅∫ 𝑥 𝑥 ∫sum/difference. Integral is called convergent if the limit exists and has a finite value and divergent if the limit doesn’t exist or has infinite value. Integrals with trigonometric functions z sinaxdx= 1 a cosax (63) z sin2 axdx= x 2 sin2ax 4a (64) z sinn axdx= 1 a cosax 2f 1 1 2; ′= −∫ ′ ∫integral of a constant: Integral of a constant \int f\left(a\right)dx=x\cdot f\left(a\right) take the constant out \int a\cdot f\left(x\right)dx=a\cdot \int f\left(x\right)dx.

Basic Integral Rules

( ) 𝑥=𝑥⋅ ( ) ∫taking a constant out: ⋅ (𝑥 ) 𝑥= ⋅∫ 𝑥 𝑥 ∫sum/difference. ′= −∫ ′ ∫integral of a constant: Integral is called convergent if the limit exists and has a finite value and divergent if the limit doesn’t exist or has infinite value. Integral of a constant \int f\left(a\right)dx=x\cdot f\left(a\right) take the constant out \int.

Derivative Rules Cheat Sheet

Integral is called convergent if the limit exists and has a finite value and divergent if the limit doesn’t exist or has infinite value. Integrals with trigonometric functions z sinaxdx= 1 a cosax (63) z sin2 axdx= x 2 sin2ax 4a (64) z sinn axdx= 1 a cosax 2f 1 1 2; ⋅ (𝑥 ) 𝑥= ⋅∫ 𝑥 𝑥 ∫sum/difference..

Basic Rules Of Integration

′= −∫ ′ ∫integral of a constant: ( ) 𝑥=𝑥⋅ ( ) ∫taking a constant out: Integral is called convergent if the limit exists and has a finite value and divergent if the limit doesn’t exist or has infinite value. Integral of a constant \int f\left(a\right)dx=x\cdot f\left(a\right) take the constant out \int a\cdot f\left(x\right)dx=a\cdot \int f\left(x\right)dx. ⋅ (𝑥 ) 𝑥=.

Solved Determine which of the integrals can be found using

Integral of a constant \int f\left(a\right)dx=x\cdot f\left(a\right) take the constant out \int a\cdot f\left(x\right)dx=a\cdot \int f\left(x\right)dx. Cheat sheet for integrals 1. ⋅ (𝑥 ) 𝑥= ⋅∫ 𝑥 𝑥 ∫sum/difference. ′= −∫ ′ ∫integral of a constant: ( ) 𝑥=𝑥⋅ ( ) ∫taking a constant out:

Page 1 of 2 Some Important Rules Of Differential & Integral Calculus

Integrals with trigonometric functions z sinaxdx= 1 a cosax (63) z sin2 axdx= x 2 sin2ax 4a (64) z sinn axdx= 1 a cosax 2f 1 1 2; ⋅ (𝑥 ) 𝑥= ⋅∫ 𝑥 𝑥 ∫sum/difference. Integral is called convergent if the limit exists and has a finite value and divergent if the limit doesn’t exist or has infinite value..

Basic Rules Of Integration

Cheat sheet for integrals 1. Integrals with trigonometric functions z sinaxdx= 1 a cosax (63) z sin2 axdx= x 2 sin2ax 4a (64) z sinn axdx= 1 a cosax 2f 1 1 2; ′= −∫ ′ ∫integral of a constant: Integral of a constant \int f\left(a\right)dx=x\cdot f\left(a\right) take the constant out \int a\cdot f\left(x\right)dx=a\cdot \int f\left(x\right)dx. ⋅ (𝑥 ) 𝑥=.

Integral cheat sheet Docsity

( ) 𝑥=𝑥⋅ ( ) ∫taking a constant out: ⋅ (𝑥 ) 𝑥= ⋅∫ 𝑥 𝑥 ∫sum/difference. Integral is called convergent if the limit exists and has a finite value and divergent if the limit doesn’t exist or has infinite value. Integral of a constant \int f\left(a\right)dx=x\cdot f\left(a\right) take the constant out \int a\cdot f\left(x\right)dx=a\cdot \int f\left(x\right)dx. Cheat sheet for.

Printable Integrals Table

Integrals with trigonometric functions z sinaxdx= 1 a cosax (63) z sin2 axdx= x 2 sin2ax 4a (64) z sinn axdx= 1 a cosax 2f 1 1 2; ( ) 𝑥=𝑥⋅ ( ) ∫taking a constant out: Cheat sheet for integrals 1. Integral is called convergent if the limit exists and has a finite value and divergent if the limit.

Basic Integral Formulas

Cheat sheet for integrals 1. ⋅ (𝑥 ) 𝑥= ⋅∫ 𝑥 𝑥 ∫sum/difference. Integral is called convergent if the limit exists and has a finite value and divergent if the limit doesn’t exist or has infinite value. ( ) 𝑥=𝑥⋅ ( ) ∫taking a constant out: Integrals with trigonometric functions z sinaxdx= 1 a cosax (63) z sin2 axdx= x.

Integrals ONE GREAT WORLD FOR ALL

Cheat sheet for integrals 1. Integral is called convergent if the limit exists and has a finite value and divergent if the limit doesn’t exist or has infinite value. ′= −∫ ′ ∫integral of a constant: ⋅ (𝑥 ) 𝑥= ⋅∫ 𝑥 𝑥 ∫sum/difference. Integrals with trigonometric functions z sinaxdx= 1 a cosax (63) z sin2 axdx= x 2 sin2ax.

Cheat Sheet For Integrals 1.

⋅ (𝑥 ) 𝑥= ⋅∫ 𝑥 𝑥 ∫sum/difference. ( ) 𝑥=𝑥⋅ ( ) ∫taking a constant out: ′= −∫ ′ ∫integral of a constant: Integral is called convergent if the limit exists and has a finite value and divergent if the limit doesn’t exist or has infinite value.