Operator Definition Math
Operator Definition Math - It tells us what to do with the value(s). A term is either a single number or a. Operators take a function as an input and give a function as an output. An operator is a symbol, like +, ×, etc, that shows an operation. A mapping of one set into another, each of which has a certain structure (defined by algebraic operations, a topology, or by an order. As an example, consider $\omega$, an operator on the set of functions. A symbol (such as , minus, times, etc) that shows an operation (i.e. The difference between an operator and a function is simply that we've decided to call the operator an operator and we've decided to.
It tells us what to do with the value(s). As an example, consider $\omega$, an operator on the set of functions. An operator is a symbol, like +, ×, etc, that shows an operation. A symbol (such as , minus, times, etc) that shows an operation (i.e. Operators take a function as an input and give a function as an output. A mapping of one set into another, each of which has a certain structure (defined by algebraic operations, a topology, or by an order. A term is either a single number or a. The difference between an operator and a function is simply that we've decided to call the operator an operator and we've decided to.
A symbol (such as , minus, times, etc) that shows an operation (i.e. The difference between an operator and a function is simply that we've decided to call the operator an operator and we've decided to. It tells us what to do with the value(s). A mapping of one set into another, each of which has a certain structure (defined by algebraic operations, a topology, or by an order. An operator is a symbol, like +, ×, etc, that shows an operation. As an example, consider $\omega$, an operator on the set of functions. Operators take a function as an input and give a function as an output. A term is either a single number or a.
"Nabla Operator Definition Math And Calculus Basics" Poster for Sale
Operators take a function as an input and give a function as an output. A mapping of one set into another, each of which has a certain structure (defined by algebraic operations, a topology, or by an order. A term is either a single number or a. A symbol (such as , minus, times, etc) that shows an operation (i.e..
Nabla operator definition, differential calculus and math Math
Operators take a function as an input and give a function as an output. A term is either a single number or a. A symbol (such as , minus, times, etc) that shows an operation (i.e. An operator is a symbol, like +, ×, etc, that shows an operation. The difference between an operator and a function is simply that.
"Nabla operator definition, math and calculus basics dark version" Art
A mapping of one set into another, each of which has a certain structure (defined by algebraic operations, a topology, or by an order. A term is either a single number or a. An operator is a symbol, like +, ×, etc, that shows an operation. As an example, consider $\omega$, an operator on the set of functions. It tells.
"Nabla Operator Definition Math And Calculus Basics" Sticker for Sale
Operators take a function as an input and give a function as an output. A symbol (such as , minus, times, etc) that shows an operation (i.e. A mapping of one set into another, each of which has a certain structure (defined by algebraic operations, a topology, or by an order. It tells us what to do with the value(s)..
Nabla operator definition, linear algebra and math Math Posters and
A symbol (such as , minus, times, etc) that shows an operation (i.e. An operator is a symbol, like +, ×, etc, that shows an operation. The difference between an operator and a function is simply that we've decided to call the operator an operator and we've decided to. It tells us what to do with the value(s). A term.
"Nabla Operator Definition Math And Calculus Basics" Poster for Sale
A mapping of one set into another, each of which has a certain structure (defined by algebraic operations, a topology, or by an order. As an example, consider $\omega$, an operator on the set of functions. An operator is a symbol, like +, ×, etc, that shows an operation. It tells us what to do with the value(s). A term.
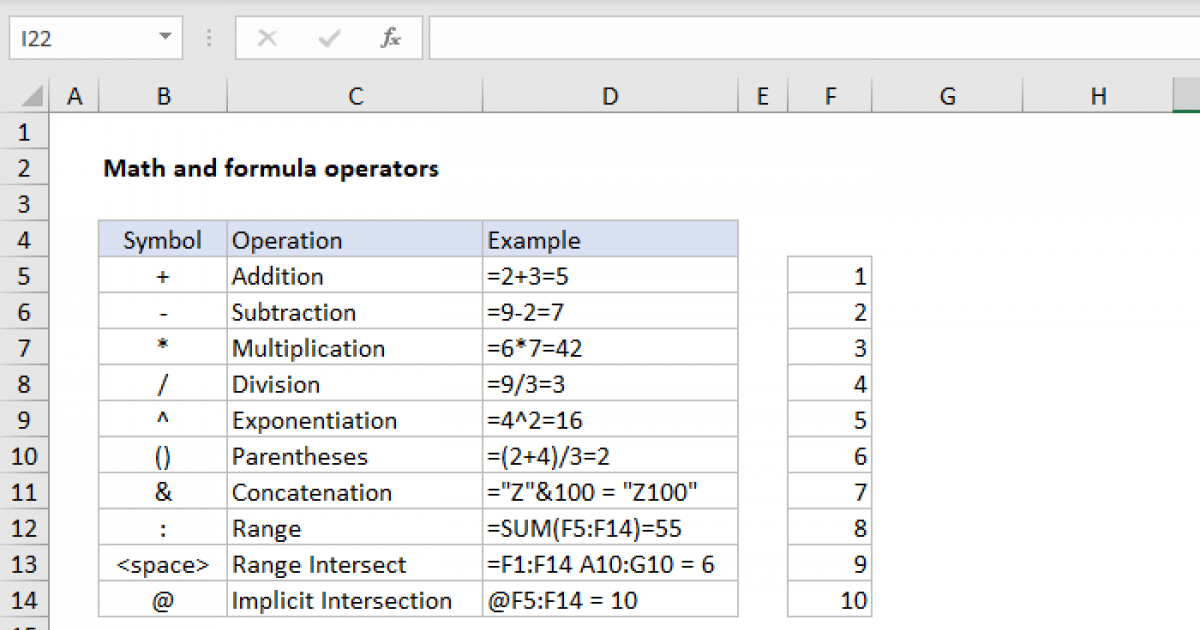
Excel Math Operators Exceljet
It tells us what to do with the value(s). A mapping of one set into another, each of which has a certain structure (defined by algebraic operations, a topology, or by an order. The difference between an operator and a function is simply that we've decided to call the operator an operator and we've decided to. As an example, consider.
"Nabla operator definition, math and physics basics" Sticker for Sale
An operator is a symbol, like +, ×, etc, that shows an operation. A symbol (such as , minus, times, etc) that shows an operation (i.e. The difference between an operator and a function is simply that we've decided to call the operator an operator and we've decided to. As an example, consider $\omega$, an operator on the set of.
"Nabla operator definition, math and calculus basics dark version
A symbol (such as , minus, times, etc) that shows an operation (i.e. The difference between an operator and a function is simply that we've decided to call the operator an operator and we've decided to. An operator is a symbol, like +, ×, etc, that shows an operation. A mapping of one set into another, each of which has.
Nabla operator definition, linear algebra and math Math Pin TeePublic
Operators take a function as an input and give a function as an output. As an example, consider $\omega$, an operator on the set of functions. A term is either a single number or a. The difference between an operator and a function is simply that we've decided to call the operator an operator and we've decided to. A symbol.
An Operator Is A Symbol, Like +, ×, Etc, That Shows An Operation.
A mapping of one set into another, each of which has a certain structure (defined by algebraic operations, a topology, or by an order. The difference between an operator and a function is simply that we've decided to call the operator an operator and we've decided to. It tells us what to do with the value(s). Operators take a function as an input and give a function as an output.
A Term Is Either A Single Number Or A.
As an example, consider $\omega$, an operator on the set of functions. A symbol (such as , minus, times, etc) that shows an operation (i.e.