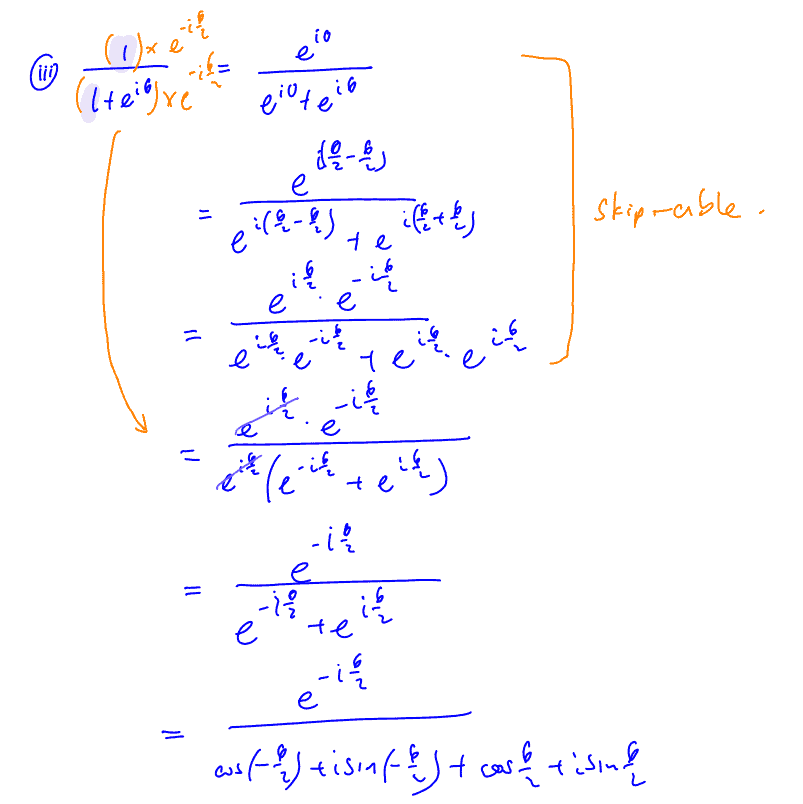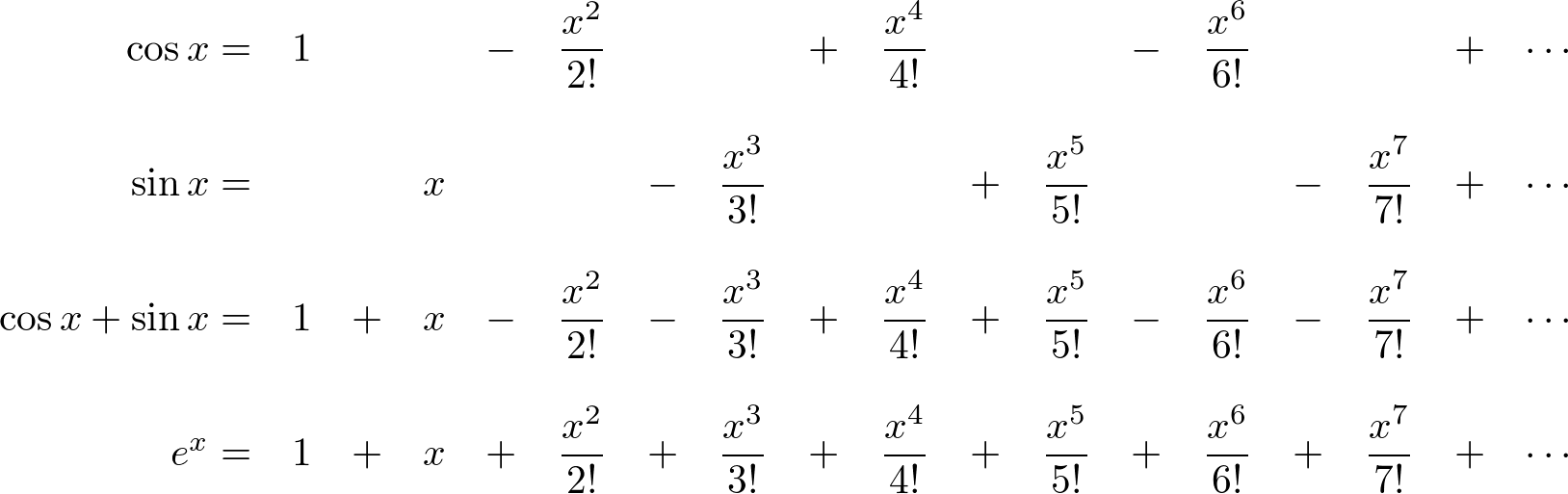Sin X In Exponential Form
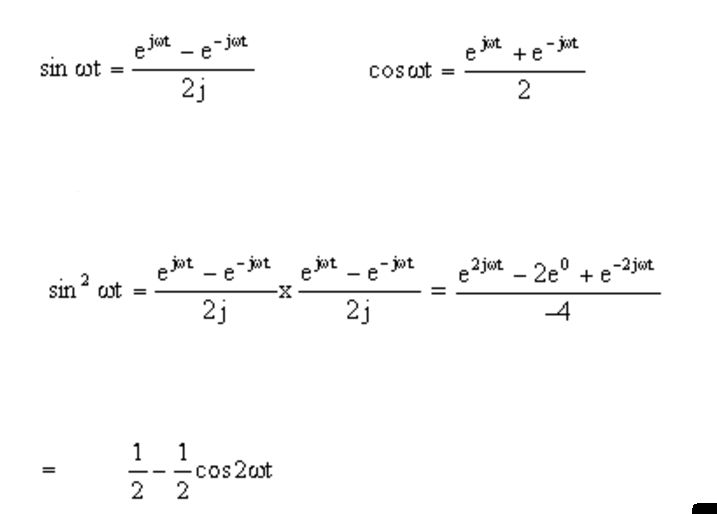
Sin X In Exponential Form - From these relations and the properties of exponential multiplication you can painlessly prove all sorts of trigonometric identities that. Euler's formula can be used to derive the following identities for the trigonometric functions $\sin{x}$ and $\cos{x}$ in terms of exponential. Sinx = eix − e−ix 2i. How do you find an expression for sin(x) in terms of eix and eix? Start from the maclaurin series of the.
How do you find an expression for sin(x) in terms of eix and eix? Sinx = eix − e−ix 2i. Start from the maclaurin series of the. Euler's formula can be used to derive the following identities for the trigonometric functions $\sin{x}$ and $\cos{x}$ in terms of exponential. From these relations and the properties of exponential multiplication you can painlessly prove all sorts of trigonometric identities that.
From these relations and the properties of exponential multiplication you can painlessly prove all sorts of trigonometric identities that. Start from the maclaurin series of the. Euler's formula can be used to derive the following identities for the trigonometric functions $\sin{x}$ and $\cos{x}$ in terms of exponential. Sinx = eix − e−ix 2i. How do you find an expression for sin(x) in terms of eix and eix?
Exponential Form of Complex Numbers
Euler's formula can be used to derive the following identities for the trigonometric functions $\sin{x}$ and $\cos{x}$ in terms of exponential. Sinx = eix − e−ix 2i. From these relations and the properties of exponential multiplication you can painlessly prove all sorts of trigonometric identities that. Start from the maclaurin series of the. How do you find an expression for.
QPSK modulation and generating signals
How do you find an expression for sin(x) in terms of eix and eix? From these relations and the properties of exponential multiplication you can painlessly prove all sorts of trigonometric identities that. Sinx = eix − e−ix 2i. Start from the maclaurin series of the. Euler's formula can be used to derive the following identities for the trigonometric functions.
Solved 5. Euler's equations are defined as sin (x) cos(x) e"
From these relations and the properties of exponential multiplication you can painlessly prove all sorts of trigonometric identities that. Sinx = eix − e−ix 2i. Euler's formula can be used to derive the following identities for the trigonometric functions $\sin{x}$ and $\cos{x}$ in terms of exponential. How do you find an expression for sin(x) in terms of eix and eix?.
Euler's exponential values of Sine and Cosine Exponential values of
Start from the maclaurin series of the. Sinx = eix − e−ix 2i. From these relations and the properties of exponential multiplication you can painlessly prove all sorts of trigonometric identities that. Euler's formula can be used to derive the following identities for the trigonometric functions $\sin{x}$ and $\cos{x}$ in terms of exponential. How do you find an expression for.
EXPONENTIAL FORM OF COMPLEX NUMBERS YouTube
Start from the maclaurin series of the. How do you find an expression for sin(x) in terms of eix and eix? From these relations and the properties of exponential multiplication you can painlessly prove all sorts of trigonometric identities that. Sinx = eix − e−ix 2i. Euler's formula can be used to derive the following identities for the trigonometric functions.
An Exponential Equation with Sine and Cosine YouTube
Sinx = eix − e−ix 2i. How do you find an expression for sin(x) in terms of eix and eix? Start from the maclaurin series of the. From these relations and the properties of exponential multiplication you can painlessly prove all sorts of trigonometric identities that. Euler's formula can be used to derive the following identities for the trigonometric functions.
Relationship between sine, cosine and exponential function Math
From these relations and the properties of exponential multiplication you can painlessly prove all sorts of trigonometric identities that. How do you find an expression for sin(x) in terms of eix and eix? Sinx = eix − e−ix 2i. Euler's formula can be used to derive the following identities for the trigonometric functions $\sin{x}$ and $\cos{x}$ in terms of exponential..
Expressing Various Complex Numbers in Exponential Form Tim Gan Math
Sinx = eix − e−ix 2i. Euler's formula can be used to derive the following identities for the trigonometric functions $\sin{x}$ and $\cos{x}$ in terms of exponential. Start from the maclaurin series of the. How do you find an expression for sin(x) in terms of eix and eix? From these relations and the properties of exponential multiplication you can painlessly.
Euler's Equation
How do you find an expression for sin(x) in terms of eix and eix? Euler's formula can be used to derive the following identities for the trigonometric functions $\sin{x}$ and $\cos{x}$ in terms of exponential. From these relations and the properties of exponential multiplication you can painlessly prove all sorts of trigonometric identities that. Start from the maclaurin series of.
A Trigonometric Exponential Equation with Sine and Cosine Math
Euler's formula can be used to derive the following identities for the trigonometric functions $\sin{x}$ and $\cos{x}$ in terms of exponential. From these relations and the properties of exponential multiplication you can painlessly prove all sorts of trigonometric identities that. How do you find an expression for sin(x) in terms of eix and eix? Start from the maclaurin series of.
From These Relations And The Properties Of Exponential Multiplication You Can Painlessly Prove All Sorts Of Trigonometric Identities That.
How do you find an expression for sin(x) in terms of eix and eix? Start from the maclaurin series of the. Sinx = eix − e−ix 2i. Euler's formula can be used to derive the following identities for the trigonometric functions $\sin{x}$ and $\cos{x}$ in terms of exponential.