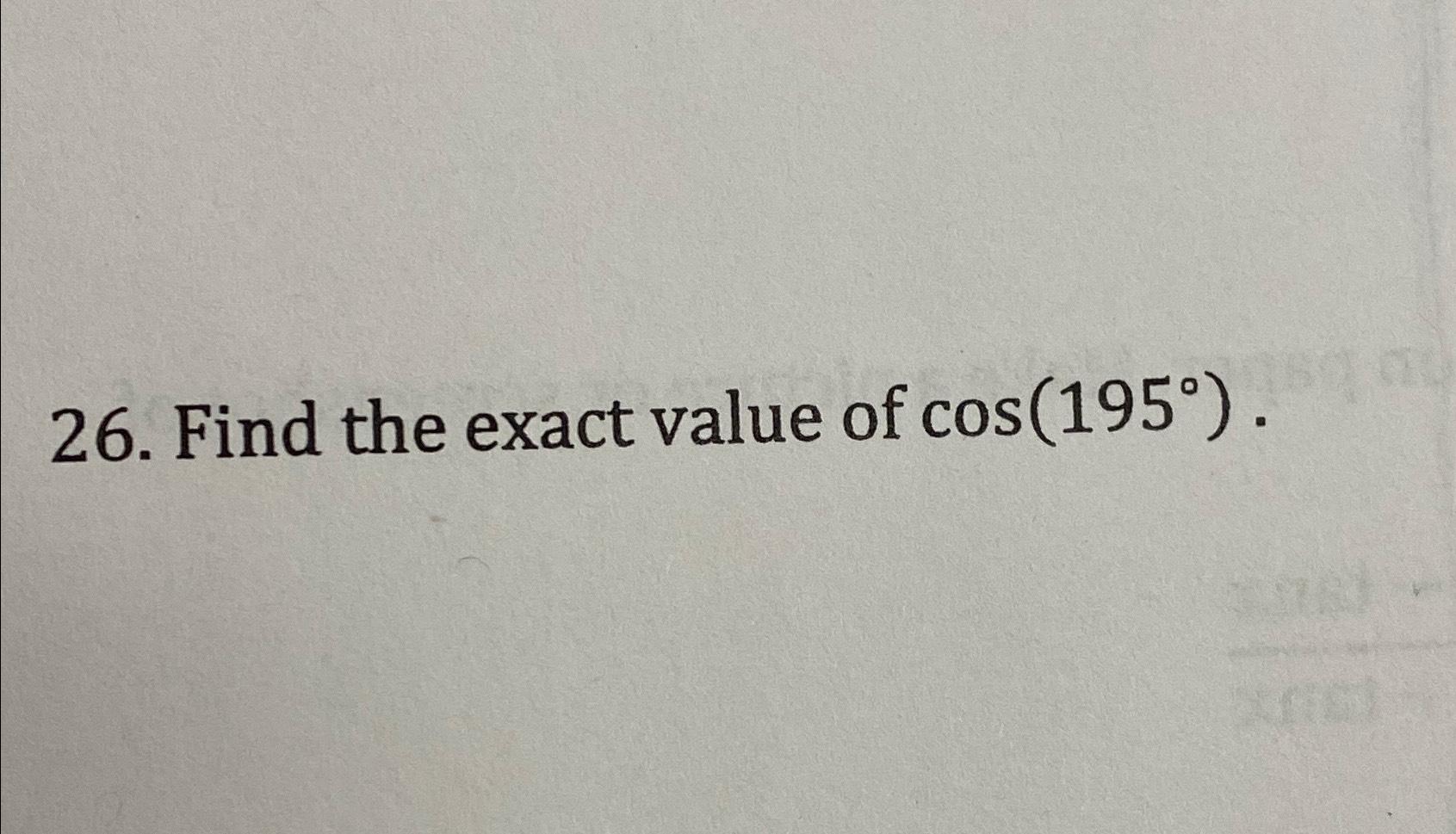What Is The Exact Value Of Cos 195
What Is The Exact Value Of Cos 195 - Using the cos(15°) exact value and switching. The exact value of cos(195°) can be found by recognizing that 195° falls in the third quadrant. Find the exact value of cos195 degrees. This is how we find that cos (195°) or cos (195° * π/180). Cos195 = cos(45 + 150). (so would #(60+135)^@#) #cos195^@ =. Hence, 195° in radians is (195*pi/180) rad. We then determine where this radian measure falls on the unit circle. 45 + 150 = 195. Find two special angles that add up to #195^@# #(30+ 165)^@#.
Cos195 = cos(45 + 150). We then determine where this radian measure falls on the unit circle. In this quadrant, cosine is negative. This is how we find that cos (195°) or cos (195° * π/180). (so would #(60+135)^@#) #cos195^@ =. Find two special angles that add up to #195^@# #(30+ 165)^@#. The exact value of cos(195°) can be found by recognizing that 195° falls in the third quadrant. The key is to write 195 degrees as the sum or difference of two numbers whose sine and cosine are known. Find the exact value of cos195 degrees. 45 + 150 = 195.
This is how we find that cos (195°) or cos (195° * π/180). We then determine where this radian measure falls on the unit circle. Find the exact value of cos195 degrees. (so would #(60+135)^@#) #cos195^@ =. Cos195 = cos(45 + 150). Find two special angles that add up to #195^@# #(30+ 165)^@#. The exact value of cos(195°) can be found by recognizing that 195° falls in the third quadrant. 45 + 150 = 195. Hence, 195° in radians is (195*pi/180) rad. Using the cos(15°) exact value and switching.
Solved Find the exact value of each expression sin 195
Hence, 195° in radians is (195*pi/180) rad. (so would #(60+135)^@#) #cos195^@ =. Using the cos(15°) exact value and switching. 45 + 150 = 195. Find two special angles that add up to #195^@# #(30+ 165)^@#.
Solved Find the exact value of cos(195°).
Using the cos(15°) exact value and switching. This is how we find that cos (195°) or cos (195° * π/180). The exact value of cos(195°) can be found by recognizing that 195° falls in the third quadrant. (so would #(60+135)^@#) #cos195^@ =. Find the exact value of cos195 degrees.
Solved Find the exact value of cos(195°)
We then determine where this radian measure falls on the unit circle. (so would #(60+135)^@#) #cos195^@ =. Find two special angles that add up to #195^@# #(30+ 165)^@#. In this quadrant, cosine is negative. The exact value of cos(195°) can be found by recognizing that 195° falls in the third quadrant.
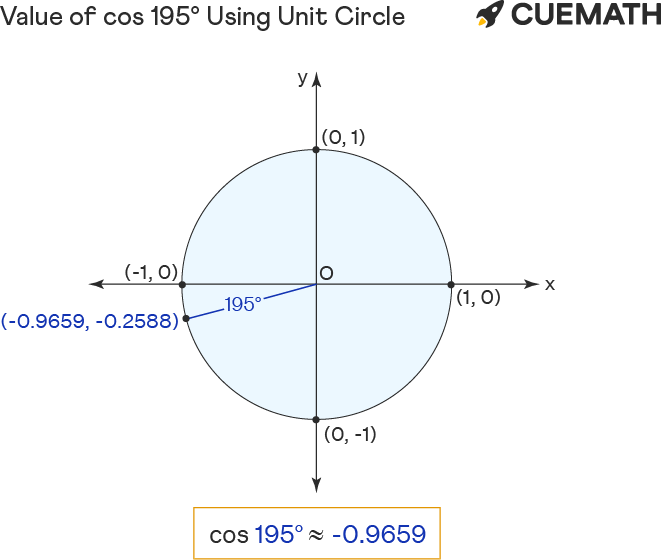
Cos 195 Degrees Find Value of Cos 195 Degrees Cos 195°
Find two special angles that add up to #195^@# #(30+ 165)^@#. Find the exact value of cos195 degrees. This is how we find that cos (195°) or cos (195° * π/180). Cos195 = cos(45 + 150). 45 + 150 = 195.
Toppr Ask Question
The exact value of cos(195°) can be found by recognizing that 195° falls in the third quadrant. Find the exact value of cos195 degrees. Cos195 = cos(45 + 150). The key is to write 195 degrees as the sum or difference of two numbers whose sine and cosine are known. Hence, 195° in radians is (195*pi/180) rad.
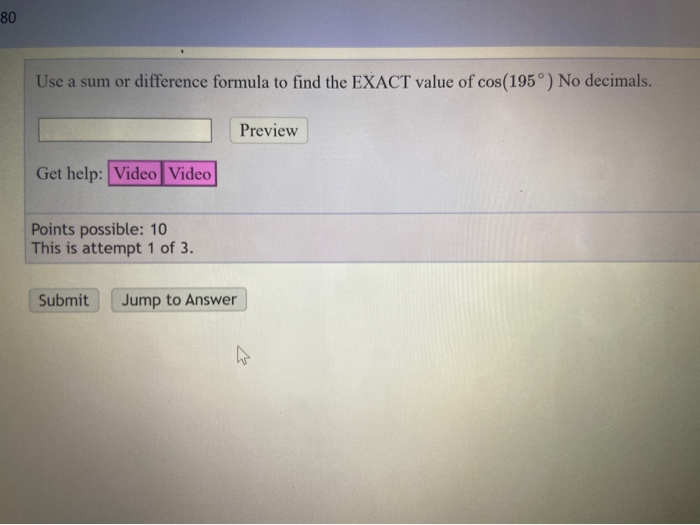
Solved Use a sum or difference formula to find the EXACT
Using the cos(15°) exact value and switching. (so would #(60+135)^@#) #cos195^@ =. 45 + 150 = 195. We then determine where this radian measure falls on the unit circle. The key is to write 195 degrees as the sum or difference of two numbers whose sine and cosine are known.
Solved 7. Find and simplify the exact value of cos(195°) by
We then determine where this radian measure falls on the unit circle. In this quadrant, cosine is negative. (so would #(60+135)^@#) #cos195^@ =. Cos195 = cos(45 + 150). Hence, 195° in radians is (195*pi/180) rad.
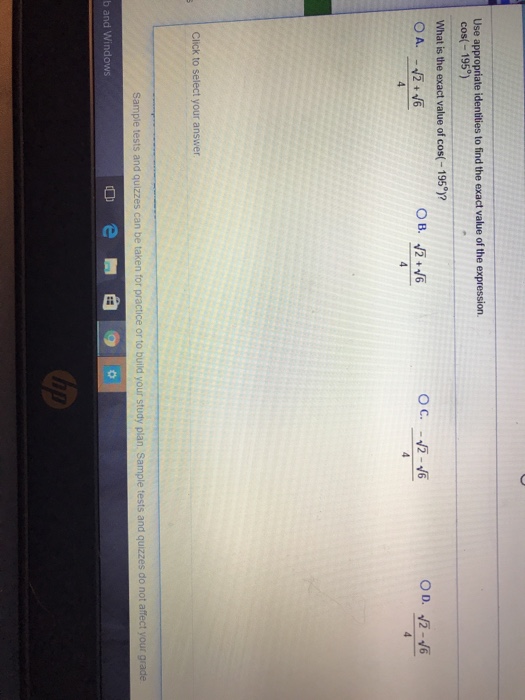
Solved Use appropriate identities to find the exact value of
Hence, 195° in radians is (195*pi/180) rad. Cos195 = cos(45 + 150). In this quadrant, cosine is negative. Using the cos(15°) exact value and switching. The exact value of cos(195°) can be found by recognizing that 195° falls in the third quadrant.
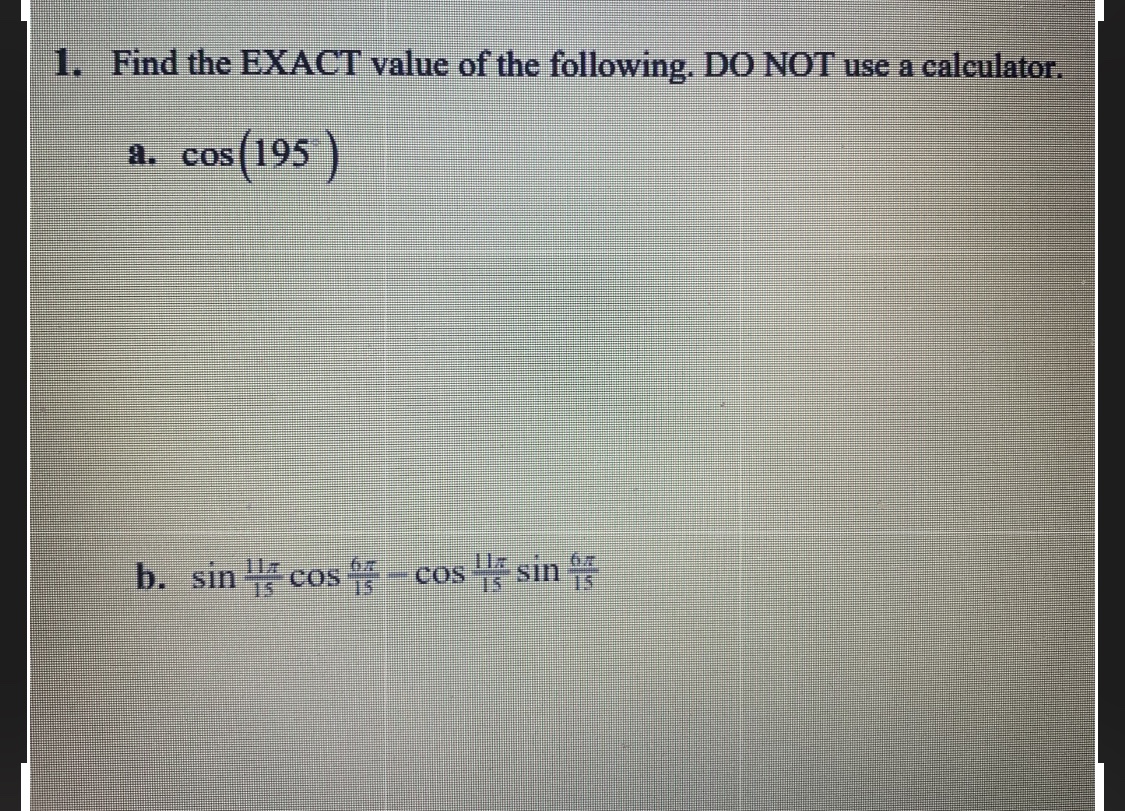
Answered 1. Find the EXACT value of the… bartleby
In this quadrant, cosine is negative. (so would #(60+135)^@#) #cos195^@ =. Cos195 = cos(45 + 150). The key is to write 195 degrees as the sum or difference of two numbers whose sine and cosine are known. Hence, 195° in radians is (195*pi/180) rad.
Solved Find the value of the product.cos 37.5 degree sin 7.5
(so would #(60+135)^@#) #cos195^@ =. We then determine where this radian measure falls on the unit circle. Find two special angles that add up to #195^@# #(30+ 165)^@#. Using the cos(15°) exact value and switching. Cos195 = cos(45 + 150).
Hence, 195° In Radians Is (195*Pi/180) Rad.
45 + 150 = 195. The exact value of cos(195°) can be found by recognizing that 195° falls in the third quadrant. This is how we find that cos (195°) or cos (195° * π/180). We then determine where this radian measure falls on the unit circle.
In This Quadrant, Cosine Is Negative.
Using the cos(15°) exact value and switching. Find two special angles that add up to #195^@# #(30+ 165)^@#. The key is to write 195 degrees as the sum or difference of two numbers whose sine and cosine are known. Find the exact value of cos195 degrees.
Cos195 = Cos(45 + 150).
(so would #(60+135)^@#) #cos195^@ =.